การเพิ่มประสิทธิภาพการออกแบบของแผงแซนวิช

การเพิ่มประสิทธิภาพของแผ่นคอมโพสิตเป็นการวิเคราะห์ที่สําคัญสําหรับรูปแบบของระบบตั้งแต่เครื่องบินไปจนถึงโครงสร้างวิศวกรรมโยธา  ความยุ่งยากในการเพิ่มประสิทธิภาพการออกแบบของความสนใจในปัจจุบันคือการลดภาระสําหรับแผ่นคอมโพสิตแซนวิช นี่คือปัญหาการเพิ่มประสิทธิภาพการออกแบบซึ่งปรับความหนาของชั้นแซนวิชให้เหมาะสมเพื่อให้น้ําหนักน้อยที่สุด สิ่งที่น่าสนใจเป็นพิเศษสําหรับร่วมสมัยดูคืองานที่เพิ่มประสิทธิภาพเค้าโครงของแผ่นแซนวิชคอมโพสิตที่มีความหนาของชั้นนอกและแกนกลางเนื่องจากตัวแปรการออกแบบ

ทฤษฎีแซนวิชสารประกอบโครงสร้างแซนวิชทั่วไปของสามชั้น  ชั้นนอกทําจากวัสดุที่มีความแข็งแรงสูง (ลามิเนตเสริมใย) ซึ่งสามารถถ่ายโอนแรงตามแนวแกนและช่วงเวลาดัดในขณะที่แกนทําจากวัสดุที่มีน้ําหนักเบาเช่นโฟมไม้ออลเดอร์ เป็นต้น วัสดุที่ใช้ในแกนแซนวิชจะต้องทนต่อการบีบอัดและสามารถส่งแรงเฉือนได้ แผ่นปกบาง ๆ เช่นชั้น 1 และ 3 มีความหนา h1 สําหรับผิวล่างและ h3 สําหรับผิวส่วนบน ความหนาของแกนคือ h2 (รูปที่ 1) ในกรณีทั่วไป h1 ไม่จําเป็นต้องเท่ากับ h3 แต่ในกรณีปฏิบัติที่สําคัญที่สุดของแซนวิชสมมาตร h1 = h3

โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต

สําหรับผลลัพธ์ N และ M การรวมจะดําเนินการเหนือแผ่นเท่านั้นและสําหรับแรงเฉือนตามขวางเหนือแกนกลาง สมการประกอบสําหรับแซนวิชเขียนในรูปแบบ hypermatrix ที่ N, M, V เป็นเวกเตอร์ของแรงปกติ

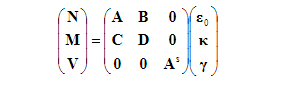
ช่วงเวลาดัดและแรงเฉือนตามขวางตามลําดับและγκε,0areเวกเตอร์ของสายพันธุ์กลางระนาบความโค้งและสายพันธุ์เฉือนขวางตามลําดับ ค่าสัมประสิทธิ์ความแข็งคํานวณจากที่_i^s_jคือโมดูลัสเฉือนขวางของแกนกลาง

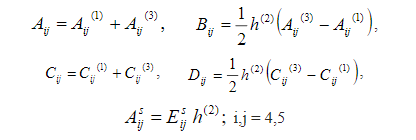
โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0Most sandwich structures can beจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0

โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0

โครงสร้างแซนวิชส่วนใหญ่สามารถจําลองและวิเคราะห์โดยใช้ทฤษฎีการเปลี่ยนรูปเฉือนสําหรับแผ่นลามิเนต [1-3]สําหรับผลลัพธ์NและMการรวมจะดําเนินการผ่านแผ่นเท่านั้นและสําหรับ thและแรงเฉือนตามขวางเหนือแกนกลาง  สมการประกอบs สําหรับแซนวิชจะเขียนในฟอร์มไฮเปอร์มาทริกซ์CkA000DC0BAในMNs0